Feb 23, 17 · x3y4z = 0 First we rearrange the equation of the surface into the form f(x,y,z)=0 x^22z^2 = y^2 x^2 y^2 2z^2 = 0 And so we have our function f(x,y,z) = x^2 y^2 2z^2 In order to find the normal at any particular point in vector space we use the Del, or gradient operator grad f(x,y,z) = (partial f)/(partial x) hat(i) (partial f)/(partial y) hat(j) (partial f)/(partial zLetf(x,y,z) = x^2y^2z^2 Calculate the gradient of f Calculate ∫_C(Fdr) where F(x,y,z)=(x,y,z) and C is the curve parametrized by r(t)=(3cos^3(t), 2sin^5(t), 2cos^13(t) for 2π≤t≤3πAnd 4z to get x2 = y2 = z2 = 2 Since x2 y2 z2 = 3 2 = 1, we get = 2 3 and thus each of x;y;z is p1 3

Solved Compute The Directional Derivative Of The Function Chegg Com
F x y z x 2 y 2 z 2 0 pde
F x y z x 2 y 2 z 2 0 pde-F~ be the vector eld F~(x;y;z) = D z 2 y2;Nov 24, 19 · Nov 24, 19 Yes there's a typo Verify Stokes theorem for F = (y^2 z^2 x^2)i (z^2 x^2 y^2)j (x^2 y^2 z^2)k over the portion of the surface x^2 y^2 2ax az = 0 While evaluating the integral we get hard to evaluate integrals What can we do to simplify this?



Answered 9 M A Y Z Xyz Xyz P 2 1 1 U Bartleby
Letting mathS/math denote the surface of integration, we need to compute the surface integral math\displaystyle \iint_S \textbf{F} \cdot d\textbf{S} \tag*{}/math in two different ways Using the Divergence Theorem (letting mathR/math dBoth of these values are greater than 1 3, leading us to believe the extremum is a minimum, subject to the given constraint Exercise 13 Use the method of Lagrange multipliers to find the minimum value of the function f(x, y, z) = x y z subject to the constraint x2 y2 z2 = 1 HintMultivariable Calculus Find the equation of the tangent plane to the surface x^2 xy y^2 z = 0 at the point (2,1,1)For more videos like this one, plea
Ie X^2 Y^2 Z^2XYYZZX=0 so (X^3 Y^3Z^3)3XYZ = (XYZ) (0) (X^3 Y^3Z^3)3XYZ=0 (X^3 Y^3Z^3)=3XYZ So value of (X^3 Y^3Z^3) is (3XYZ) read less 1 Comments Dislike Bookmark Maniyar Deval Tutor Here, we use formula of x^3y^3z^3=(xyz)(x^2y^2z^2xyyzzx) Then x^2y^2z^2=xyyzzx is given to put theDec 04, 13 · Use Stokes' Theorem to evaluate ∫C F · dr where C is oriented counterclockwise as viewed from above F(x, y, z) = (x y^2)i (y z^2)j (z x^2)k, C is the triangle with vertices (5, 0, 0), (0, 5, 0), and (0, 0, 5)Oct 13, 09 · Optimize f(x,y,z) = x 3 y 3 z 3, subject to the constraint g(x,y,z) = x 2 y 2 z 2 1 = 0 Step 1 I did L = f tex\lambda/texg = x 3 y 3 z 3 tex\lambda/tex(x 2 y 2 z 2 1) Step 2 I got L x = 3x 2 2tex\lambda/texx = 0, L y = 3y 2 2tex\lambda/texy = 0, L z = 3z 2 2tex\lambda/texz = 0 Now I can't seem to solve these 3 equations to get the critical
If U = F ( Y − X X Y , Z − X X Z ) , Show that X 2 ∂ U ∂ X Y 2 ∂ U ∂ Y Z 2 ∂ U ∂ Z = 0 University of Mumbai BE Biomedical Engineering Semester 1 (FE First Year) Question Papers 141 Important Solutions 526 Question Bank Solutions 528 Concept Notes 24 TimeS is defined as a sphere However, when I type "S f(x,y,z) = 1" into the input bar, nothing is graphed and the algebra window shows S as an undefined Implicit CurveLet's now return to the problem that we started before the previous theorem Using Implicit Differentiation of a Function of Two or More Variables and the function f (x, y) = x 2 3 y 2 4 y − 4, f (x, y) = x 2 3 y 2 4 y − 4, we obtain
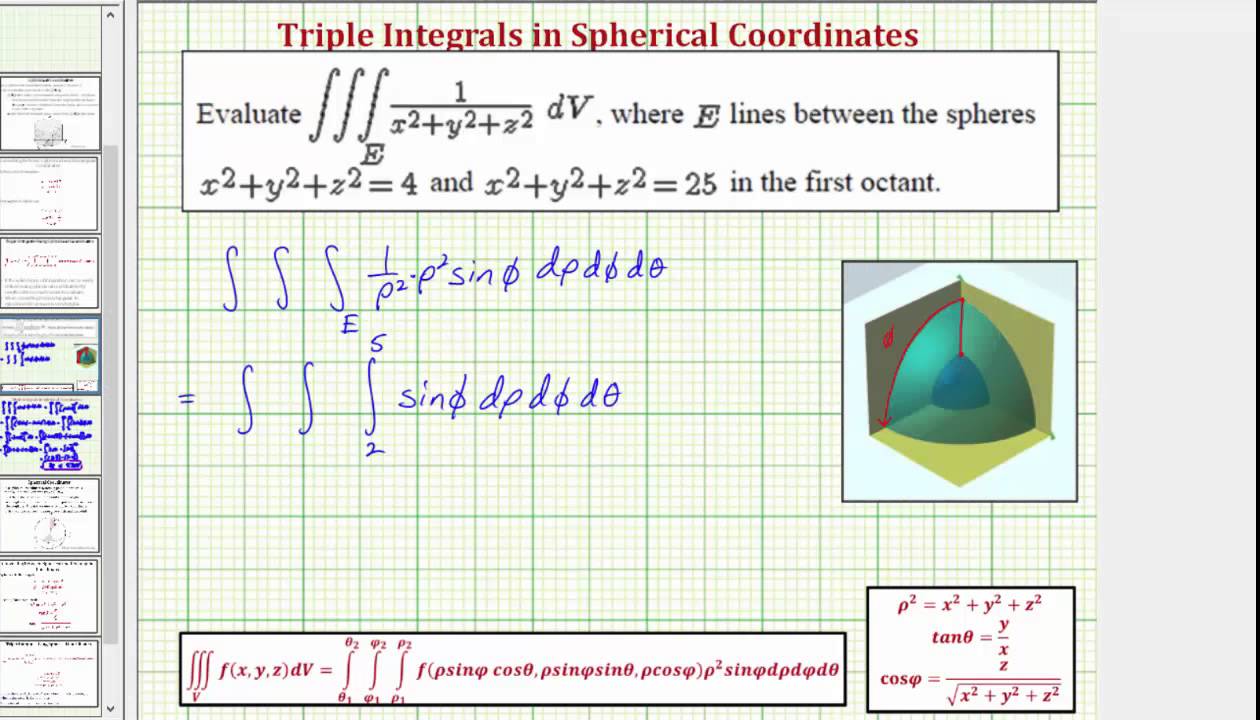


Evaluate A Triple Integral Using Spherical Coordinates Triple Integral Of 1 X 2 Y 2 Z 2 Youtube
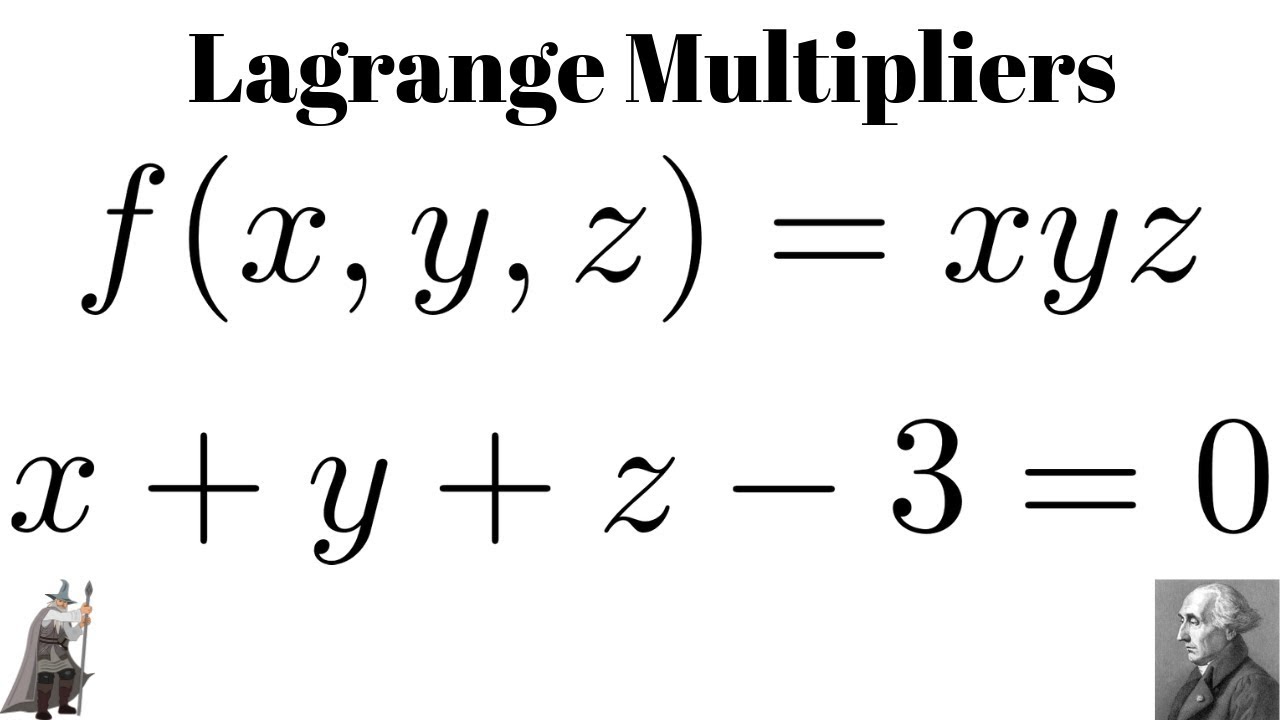


Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube
Puoi applicare il teorema della divergenza e calcolarlo come SSS_D (112z) dV = 2 SSS_D (1 z ) dV In coordinate cilindriche D è descritto da 0Let f x y z x 2 sin z x 2 y 2 z 2 1 a Find f x y z and evaluate f 1 1 0 b Find from MATH 324 at University of WashingtonF(xy,z) = x 2 y 2 z The level surfaces are the parabaloids z = c x 2y 2 Example 4 Suppose we have f(x,y,t) = cos(t) e x 2 y 2 which represents the temperature at any pt on a rectangular plate in the plane At each fixed t 0 we have a function of 2 variables f(x,y,t 0) = cos(t 0) e x 2 y 2 For example below is the temperature profile


Contourplot And 3dplot Of F X Y Z X Z Y Z X Y Z Mathematica Stack Exchange



Solved Problem 1 12 Points Let F X Y X2 Y2 A F Chegg Com
If Z=F(XY) X=R Cos θ, Y=R Sinθ Prove that ( ∂ Z ∂ X ) 2 ( ∂ Z ∂ Y ) 2 = ( ∂ Z ∂ R ) 2 1 R 2 ( ∂ Z ∂ θ ) 2When I type "S x^2 y^2 z^2 = 1" into the input bar, this works perfectly;Z = −1, y = −x



Solutions To Homework Assignment 4 Math Pdf Free Download



Homework Assignment 4 Math 253
We think you wrote (2xy3z2xy^2z/(x^2yy^2zxz^2))*x^2yy^2zxz^2 This deals with adding, subtracting and finding the least common multipleThe paraboloid y = x z is shown in blue and orange The paraboloid x = y z is shown in cyan and purple In the image the paraboloids are seen to intersect along the z = 0 axis If the paraboloids are extended, they should also be seen to intersect along the lines z = 1, y = x;Evaluate the surface integral Ils Fids for the given vector field F and the oriented surface S In other words, find the flux of F across S For closed surfaces, use the positive (outward) orientation F (x, y, z) = x2 i y2 j z2k S is the boundary of the solid halfcylinder 0



One Dimentional Wave Eqn



Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5
Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeX 2z2 dS, where Sis the part of the cone z2 = x2 y between the planes z= 1 and z= 3 The widest point of Sis at the intersection of the cone and the plane z= 3, where x2 y2 = 32 = 9;F= ey2i(y sin(z2))j(z −1)k, and S is the upper hemisphere x 2 y 2 z 2 = 1, z ≥ 0, oriented upward Note that the surface S does NOT include the bottom of the hemisphere



Qbankmat2sem



Calc3 1001 By James Bardo Issuu
WolframAlpha brings expertlevel knowledge and capabilities to the broadest possible range of people—spanning all professions and education levelsRewrite (x−y −z)2 ( x y z) 2 as (x−y−z)(x−y−z) ( x y z) ( x y z) Expand (x−y−z)(x−y−z) ( x y z) ( x y z) by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply x x by x xCheck out a sample textbook solution See solution arrow_back Ch 145 Suppose that the equation F(x, y, z) = 0 Ch 145 Equation



Solved F Yz Xz Z 3 That Part Of The Cone Z Squ Chegg Com



Solved 113 Section 16 8 Stokes Theorem 10 F X Y Z 2y Chegg Com
Dec 27, 16 · See below Calling Sigma>f(x,y,z)=y^2 3 x^2 z^2 4=0 and considering p = (x,y,z) such that p in Sigma, we have vec n = (pp_1) xx (pp_2) is a vector normal to the plane Pi defined by the points p, p_1, p_2 Now, the vector vec n can be computed over Sigma as grad f = ((partial f)/(partial x), (partial f)/(partial y), (partial f)/(partial z)) =2(3x,y,z) The Sigma tangentThe triple integral of a function f(x, y, z) over a rectangular box B is defined as lim l, m, n → ∞ l ∑ i = 1 m ∑ j = 1 n ∑ k = 1f(x ∗ ijk, y ∗ ijk, z ∗ ijk)ΔxΔyΔz = ∭Bf(x, y, z)dV if this limit exists When the triple integral exists on B the function f(x, y, z) is said to be integrable on BPlot x^2 3y^2 z^2 = 1 Extended Keyboard;



Vectors And The Geometry Of Space Monografias Com



Answered 14 F X Y Z X Y 4z X Y Bartleby
Get answers by asking now Ask question 100 Join Yahoo Answers and get 100 points today Join Trending questions Trending questions is tangent to circle A at point G If AG = 8 and GI = 15, determine the length of ?Jun 01, 19 · Verify GDT for vector F = (x^2 yz)vector i (y^2 zx)j (z^2 xy)k taken over the rectangular parallelepiped 0 ≤x ≤ a, 0 ≤ y ≤ b, 0 ≤ z ≤ cClick here👆to get an answer to your question ️ If x^2 = y z, y^2 = z x, z^2 = x y , then the value of 1x 1 1y 1 1z 1 is



Let Math F X Y Z X 2 Y 2 Z 2 Kyz Math A Verify That Math 0 0 0 Math Is A Critical Point For Math F Math B Find All Values Of Math K Math Such



Solved Compute The Directional Derivative Of The Function Chegg Com
Jun 01, 19 · Find a unit tangent vector to the following surfaces at the specified points x = t^2 1, y = 4t 3, z = 2t^2 6t at t = 2 asked Jun 1, 19 in Mathematics by Taniska (And the CauchyRiemann equations hold at each z 2 C;Then f(z) = z jzj2 = x x2 y2 i y x2 y2;



If U F R Where R 2 X 2 Y 2 Then 2u X 2 2u Y 2



Answered 9 M A Y Z Xyz Xyz P 2 1 1 U Bartleby
Question F1(x,y,z) = X^2 y^2 z^2 −1 = 0 F2(x, Y, Z) = 2x^2 Y^2 − 4z = 0 F3(x,y,z) = 3x^2 −4yz^2 = 0 This System Can Be Concisely Represented As F(x) = 0, Where F(x) = (f1, F2, F3)T , X=(x,y,z)T And 0 = (0,0,0)T (transpose Written Because These Should Be Column Vectors) Using Matlab Starting With The Initial Condition X0 = (05, 05, 05)T , ImplementThe problem is I have to find all the possible combination of integers (x, y, z) that will satisfy the equation x^2 y^2 z^2 = N when you are given an integer N You have to find all the unique tuples (x, y, z) For example, if one of the tuple is (1, 2, 1), then (2, 1, 1) is not unique anymore1 (Exercise 12) Find the maximum and minimum of f(x;y;z) = x4 y4 z4 subject to the constraint x 2y2 z = 1 Solution We have ∇f(x;y;z) = 4x3;4y3;4z3 = 2 x;2 y;2 z = ∇g(x;y;z) Case 1 If all of x;y;z ̸= 0, we can divide 4x3 = 2 x, 4y3 = 2 y, 4z3 = 2 z by 4x;4y;
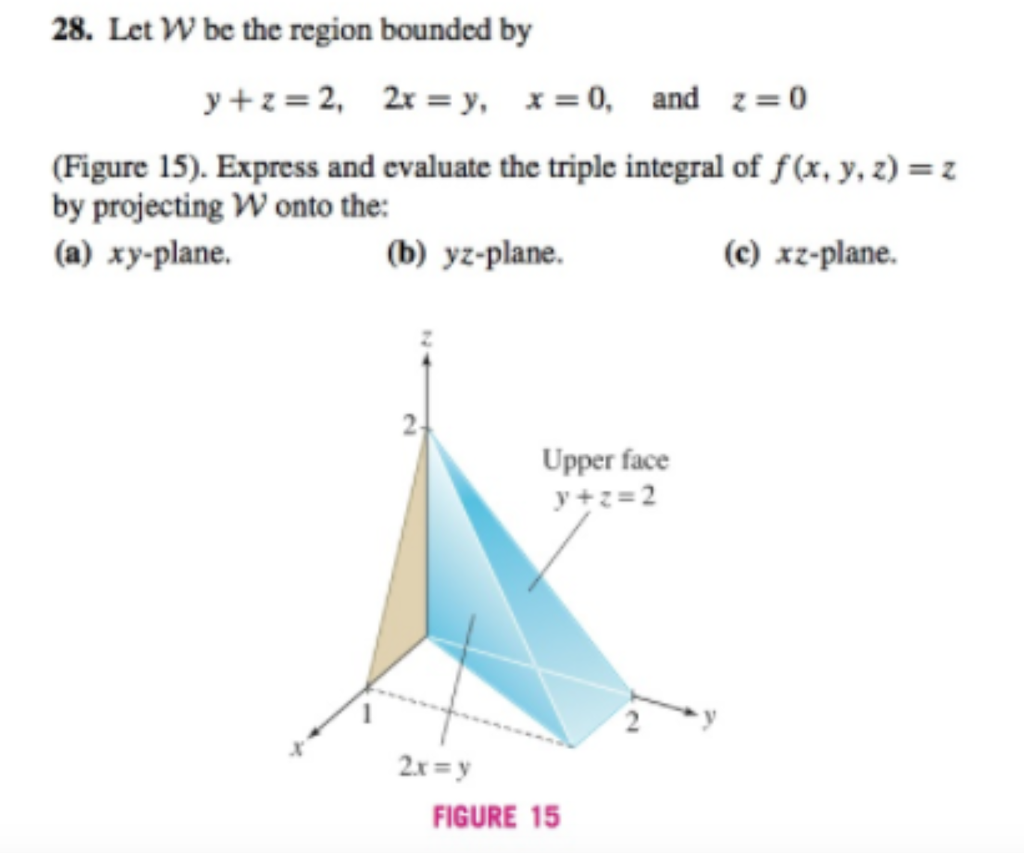


Solved 28 Let W Be The Region Bounded By Y Z 2 2x Y X Chegg Com



Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z
In this case it will work, as the coefficients of x2 and y2 are equal, so that the terms 2cosθsinθX Y will cancel We have x^2y^2=36z^2 and xy=10z, which gives (10z)^22xy=36z^2 or xy=3210zz^2 and xyz=32z10z^2z^3 Also, (xy)^2\geq4xy, which gives 3z^2z28\leq0 or 2\leq z\leq\frac {14} {3}Clearly given f = (r^2)^(n) = r^(2n) where r = sqrt(x^2 y^2 z^2) = r Now as we know that grad(f) = f´(r) (r/r) ==> div(grad(f)) =div(f´(r) r/r)={grad(fClick here👆to get an answer to your question ️ If x^2 y^2 z^2 xy yz zx = 0 then the value of x yz
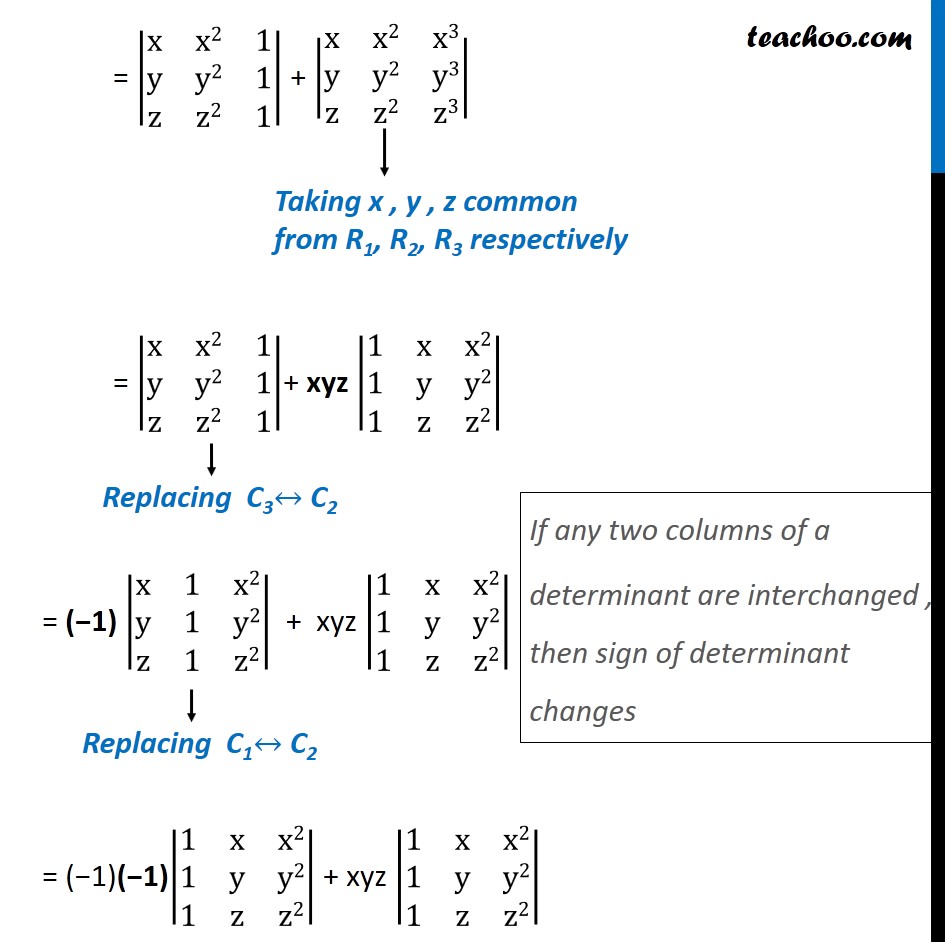


Example 15 If X Y Z Are Different Show 1 Xyz 0 Class 12
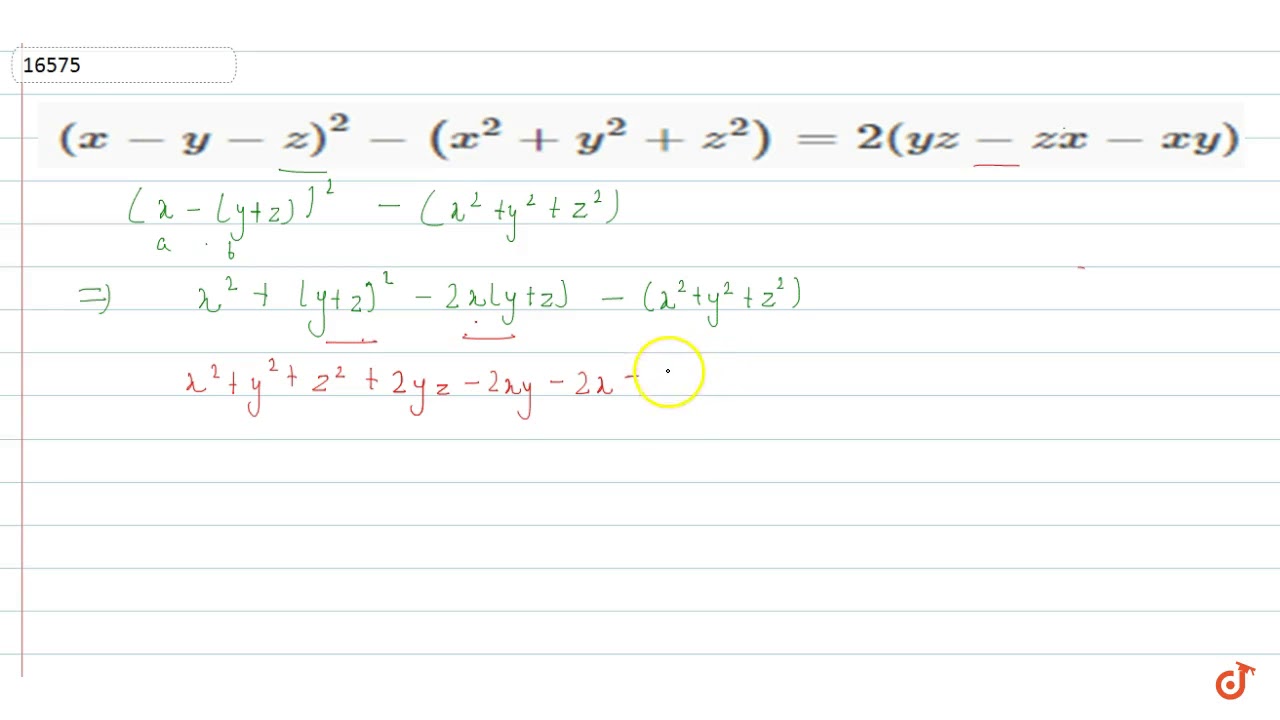


X Y Z 2 X 2 Y 2 Z 2 2 Yz Zx Xy Youtube
Minimize the function f(x, y, z)=x^{2}y^{2}z^{2} subject to the constraints x2 y3 z=6 and x3 y9 z=9 Video Transcript So the question is gonna look a little bit different We instead of having one constraints, we're gonna find extreme valueIf cos(xyz) = 1 x 2 y 2 z 2, find ∂ z ∂ x and ∂ z ∂ y check_circle Expert Solution Want to see the full answer?Its thinnest point is where x 2 y = 12 = 1 Thus, Sis the portion of the surface z= p x2 y2 over the region D= f(x;y) 1 x2 y2 9g So ZZ S x2z2 dS = ZZ D



Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z



Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube
Answer to Find the work done by the force field F(x, y, z) = \{x y^2, yz^2,z x^2\} on a particle moving along the line segment from (0,0,1)F(y,x 1,x 2)=0 where the partial derivatives are ∂F/∂x 1 = F x 1, ∂F/∂x 2 = F x 2 and ∂F/∂y = F yThis class of functions are known as implicit functions where F(y,x 1,x 2)=0implicity define y = y(x 1,x 2) What this means is that it is possible (theoretically) to rewrite to get y isolated and expressed as a function of x 1 and x 2A) it amounts to solving in Z x 2 y 2 = 3 z 2 You have that x 2 y 2 = 0 (m o d 3) → x = y = 0 (m o d 3), and you get back the original one using descending method, and this proves x = y = z = 0



Vector Analysis By Alimkanwalimtinaa Issuu



Pdf The Damascus Inequality
2xy;e p zcosz E Evaluate Z C F~d~r Solution The line integral is very di cult to compute directly, so we'll use Stokes' Theorem The curl of the given vector eld F~is curlF~= h0;2z;2y 2y2i To use Stokes' Theorem, we need to think of a surface whose boundary is the given curve C First, let'sSo that u(x;y) = x x2 y2 and v(x;y) = y x2 y2 for z 6= 0 Now, @u @x = y2 x2 (x2 y2)2 = @v @y and @u @y = 2xy (x2 y2)2 = @v @x Since the partial derivatives are all continuous at each z 2 C;Let {eq}f(x,y,z)=x^2y^2z^2 {/eq} and let S be the level surface defined by f(x,y,z) = 4 (a) Find an equation for the plane tangent to S at {eq}P_{0}(1,1,2)



Find The Centre And Radius Of The Circle X 2 Y 2 Z 2 9 X Y Z 3



If Xyz 1 X 1 Y 1 Z Where 0 Lt X Y Z Lt 1 Then The Minimum Value Of X 1 Z Y 1 X Z Youtube
(a) If f(z) = 1 z;Y Simplify —— x 2 Equation at the end of step 1 y (((((x 2)(y 2))(z 2))(2x•——))y 2)z 2)2xz x 2 Step 2 Rewriting the whole as an Equivalent Fraction 21 Subtracting a fraction from a whole Rewrite the whole as a fraction using x as the denominatorCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Chapter 14 By Faheem Ajmal Issuu



Answered 3j 8 F X Y Xin Y P 3 1 U 5 13 Bartleby
Aug 12, 11 · f(x^2y^2,zxy) = 0 > x^2 y^2 z xy = 0 then the pde is 2x y 2y x 1 = 0 x y 1 = 0 0 0 Still have questions?



Solutions To Homework Assignment 4 Math Pdf Free Download



Vector Analysis By Alimkanwalimtinaa Issuu



Tangent Plane To X 2 Xy Y 2 Z 0 Youtube



Por Favor Me Ajudemx Y Z 1 2x 4y 2z 16 Y Z 3 Brainly Com Br
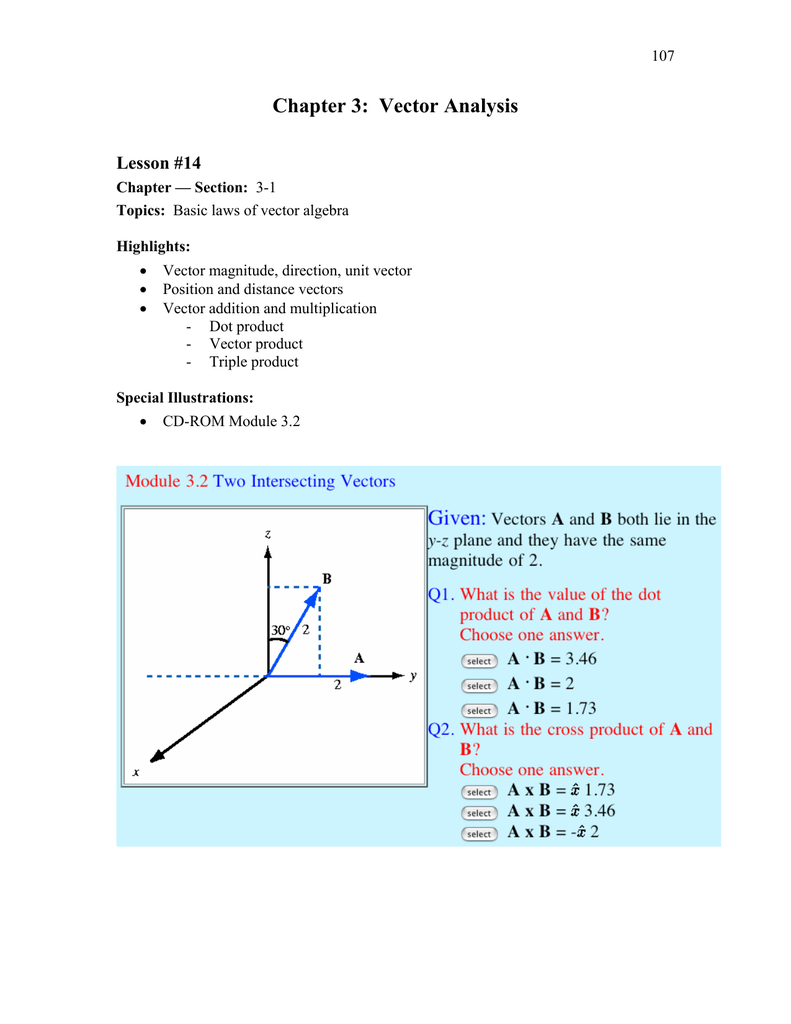


Chapter 3 Vector Analysis


Solved 6 Find The Maximum Value Of The Function F X Y Z Xyz On The Sphere X2 Y2 Z2 12 8 4 0 4 8 None Of These Rm 9 0 9 S 7 Maximi Course Hero



Math 6c Chapter 12 Quiz



Using Nabla With Partial Derivatives And The Laplace Operation Partial X 2 Partial Y 2 Partial Z 2 Mathematics Stack Exchange



Several Variable Calculus Docsity



If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3 Youtube



Prove That Determinant Of X X2 Yz Y Y2 Zx X Y Y Z Z X Xy Yz Zx Z Z2 Xy Brainly In



Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z



If X Y Z 1 X Y Y Z Z X 1 And X Y Z 1 Find The Value Of X 3 Y 3 Z 3dot Youtube



Example 32 Show That Determinant 2xyz X Y Z 3 Class 12



If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video



Lagrange Multipliers Ppt Download



Example 15 If X Y Z Are Different Show 1 Xyz 0 Class 12



X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In



Solutions To Assignment 7



Vectors And The Geometry Of Space Monografias Com



Solved Find The Mass And Center Of Mass Of The Solid E Wi Chegg Com



Solved I Really Need Help Finding V X Y The Rest Is Corr Chegg Com



If X 2 Y 2 Z 2 2 X Y Z 3 Find The Value Of 2x 3y 4z Youtube
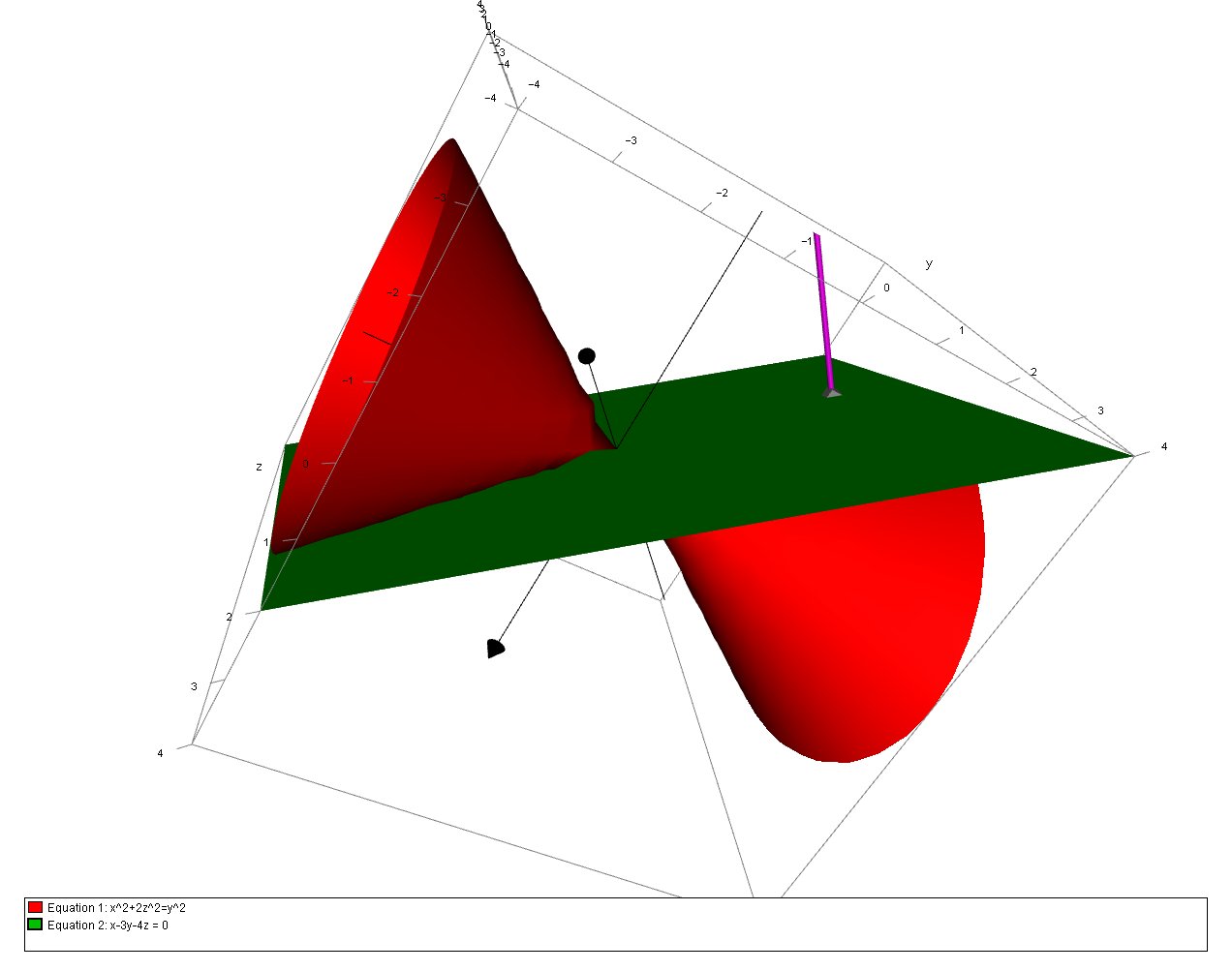


How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic



2 Partial Differentiation



Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5



X Y Z 2 Y Z X 2 Z X Y 2 0 Then Find X Y Z Brainly In



Example 15 If X Y Z Are Different Show 1 Xyz 0 Class 12



Solved F X Y Z Dv 6 1 4 Find 1 F X U Z V Chegg Com



Solved 2 Use The Divergence Theorem To Find The Outward Chegg Com



Solve The Following System Of Equation By Matrix Method 1 X Y Z 6 X Y Z 4 X 2y 2z 1 2 X Y 3z 10 X Y Z 2 2x 3y 4z 4 3 X Y Z 6 X 2y 3z 6 X Y Z 2 4 2x Y Mathematics Topperlearning Com Yv1op566



Maxiam Minima With Side Condition Maxima And Minima Analysis



Practice Problems For Final



Solved Verify That The Divergence Theorem Is True For The Chegg Com



Solved Given F X Y Z X 2 Y X Z 4 Find F 3 5 2 Chegg Com



Calc 501 1000 By James Bardo Issuu



Example 15 If X Y Z Are Different Show 1 Xyz 0 Class 12



If X 2 Y 2 Z 2 R 2 And X Y Z 0 Then Tan 1 Xy Z



If X Y Z 0 Then Prove That X 2 Yz Y 2 Zx Z 2 Xy 3 Brainly In



Solved 1 Draw The Tree Diagram For The Chainrule And Wr Chegg Com



Vectors Gradient Divergence And Curl Pdf Free Download



Ejercicio 1 1



Systems Engineering And Analysis Ppt Download



Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z



1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download
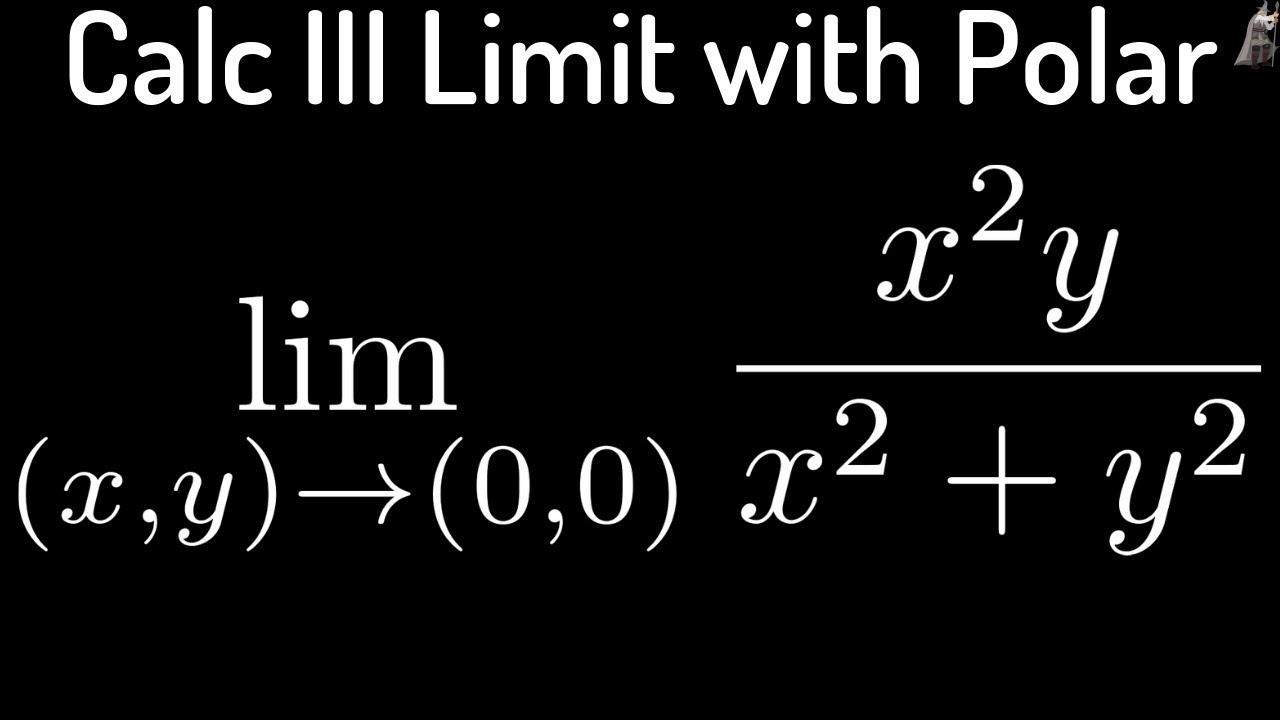


Multivariable Calculus Limit Of X 2y X 2 Y 2 Using Polar Coordinates Youtube



Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5



How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube



Solved Please Try And Answer All Of Them Show All Work Chegg Com



Creating A Successful Cv Dk Publishing 09 Subtraction Equations



Using Cramer S Rule Solve 1 X 1 Y 1 Z 1 2 X 5 Y 3 Z 0 1 X 2 Y 4 Z 3 Youtube
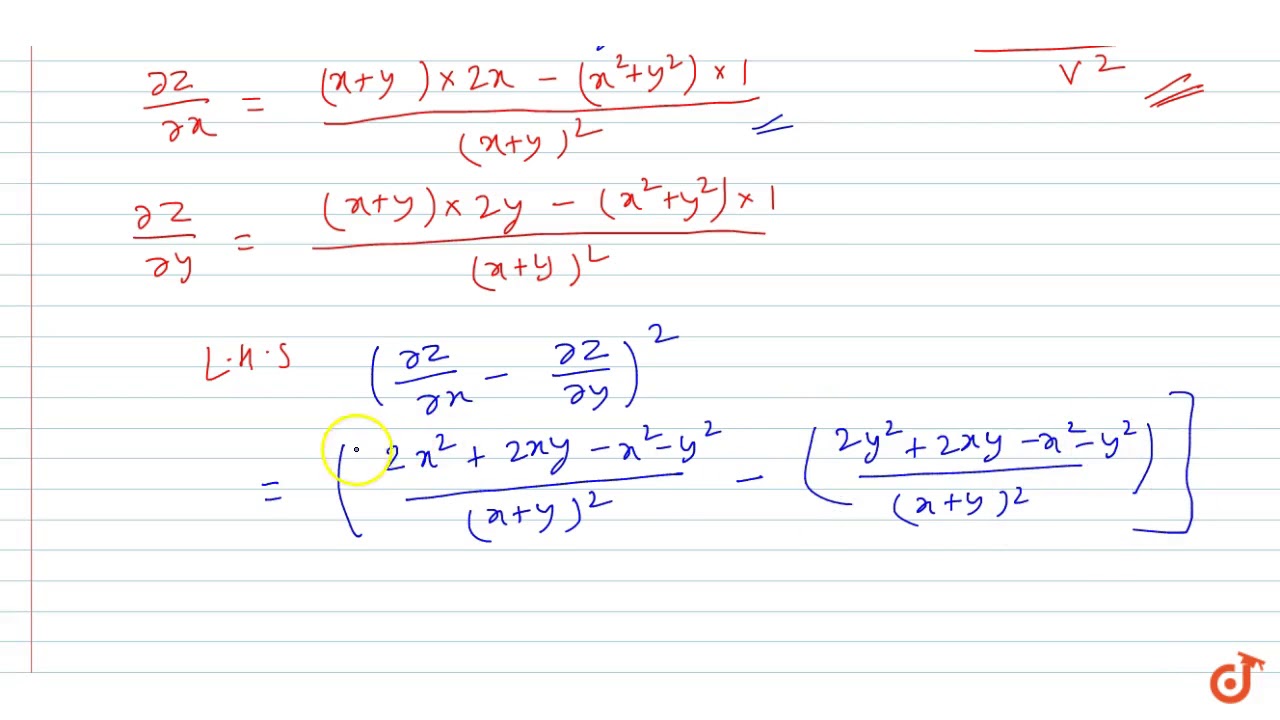


If Z X Y X 2 Y 2 Show That Delz Delx Delz Dely 2 4 1 Delz Delx Del Youtube



Line Integrals In Conservative Field Studocu
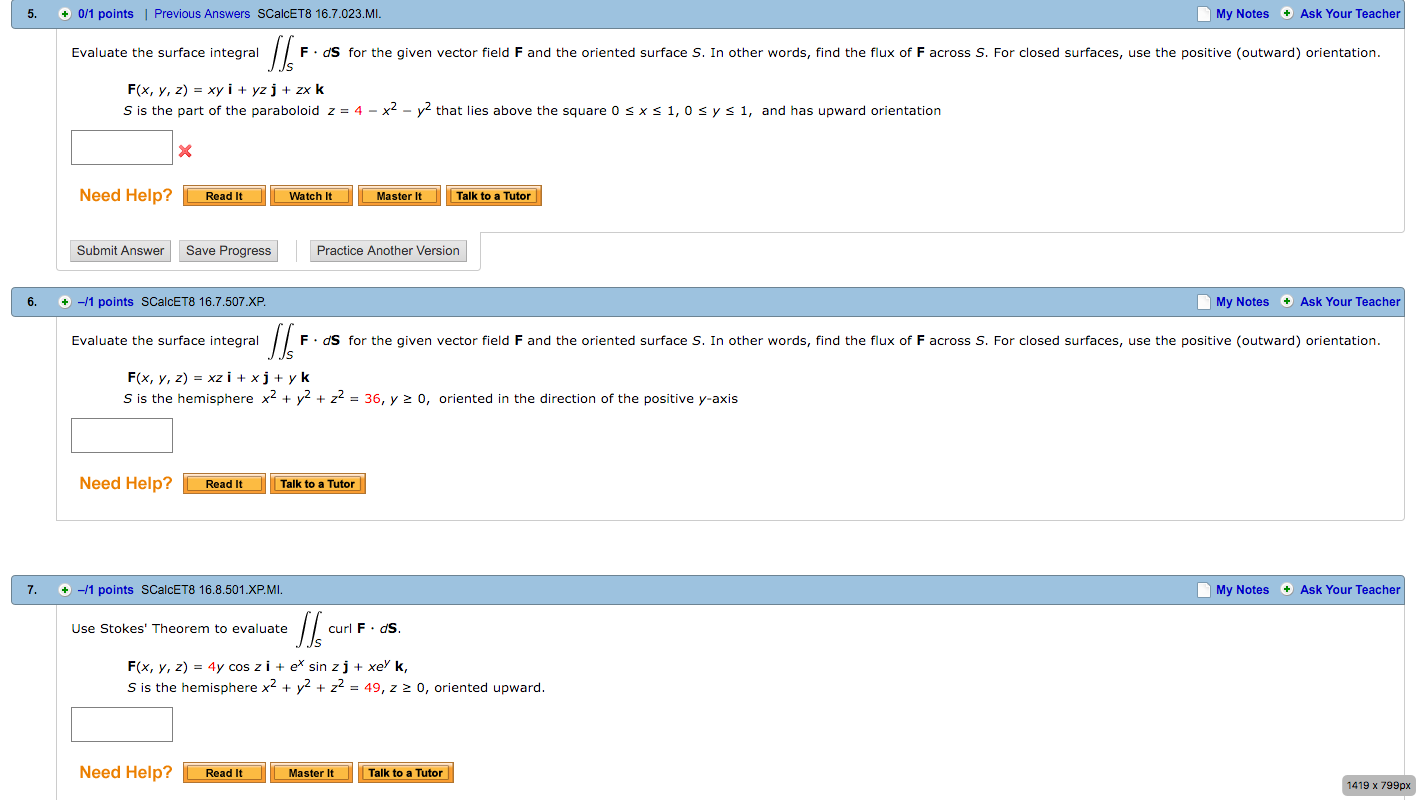


Solved Evaluate The Surface Integral Doubleintegral S F M Chegg Com



Chapter 16 1 16 3 Solutions Rogowski Pdf Document



Lagrange Multipliers Minimize F X Y X 2 Y 2 Subject To X 2y 5 0 Youtube



Integrales Triples



Solved I Need Help With The Following Questions Really S Chegg Com



0 件のコメント:
コメントを投稿